核心思想 数据结构的职责就是增删查改。寻找所有可能情况,对所有可能情况做解。
二分法
做类似题型,需要分辨出题目提供的条件是否会导致:超出索引、超出类型 (int → long long),或采用其他整型计算方法求解。
关于数组
数组中间插入(insert)元素 → 其需要经历数据搬移,时间复杂度为 O(N)。
// 大小为 10 的数组已经装了 4 个元素
int arr[10];
for (int i = 0; i < 4; i++) arr[i] = i;
// 在索引 2 置插入元素 666
for (int i = 4; i > 2; i--) arr[i] = arr[i - 1];
arr[2] = 666;删除中间元素 → 涉及「数据搬移」。
// 删除 arr[1]
for (int i = 1; i < 4; i++) arr[i] = arr[i + 1];
arr[4] = -1;关于二分搜索框架
相错终止类型 (相等返回)
相等返回只解决数组中仅有 ≤1 个目标元素,如果对应有多个元素寻找边界就会寻找不全。
class Solution {
public int search(int[] nums, int target) {
int l = 0, r = nums.length - 1;
while(l <= r){
int c = l + (r - l) / 2;
if(nums[c] == target) return c;
else if(nums[c] < target) l = c + 1;
else r = c - 1;
}
return -1;
}
}模板一:相错终止
- 初始:l=0, r=n-1 (左闭右闭)
- 循环:while (l <= r)
- 更新:l = c+1 / r = c-1
模板二:相等终止
- 初始:l=0, r=n (左闭右开)
- 循环:while (l < r)
- 更新:l = c+1 / r = c
寻找边界
寻找左侧边界(如果 target 不存在,返回大于 target 的最小索引):
int left_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) right = mid;
else if (nums[mid] < target) left = mid + 1;
else if (nums[mid] > target) right = mid;
}
return left;
}双指针 (数组)
快慢指针
快慢指针,就是两个指针同向而行,一快一慢。
- 快指针:寻找新数组的元素(不含目标元素的数组)。
- 慢指针:指向更新新数组下标的位置。
同时可以利用慢指针作为数组的长度进行截断返回,减少内存利用。
滑窗
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
只用一个for循环,那么这个循环的索引,一定是表示滑动窗口的终止位置。
重要点
- 窗口内是什么?
- 如何移动窗口的起始位置?(如:当前窗口值 >= s,缩小窗口)
- 如何移动窗口的结束位置?(遍历指针)
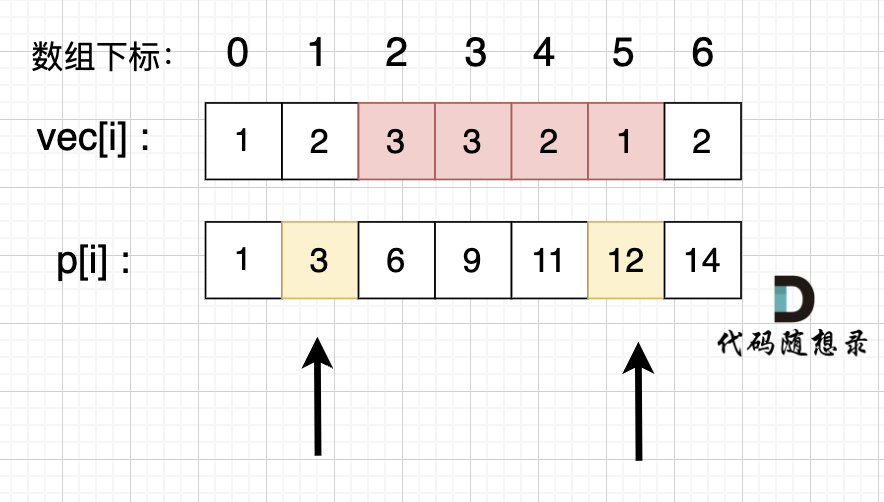
前缀和
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
int main(){
int n, a, b;
cin >> n;
vector<int> sum_array(n);
int sum = 0;
// 构建前缀和
for(int i = 0; i < n; i ++){
int val; cin >> val;
sum += val;
sum_array[i] = sum;
}
// 区间查询
while(cin >> a >> b){
// 注意处理边界
cout << sum_array[b] - sum_array[a] + array[a] << endl;
}
}
链表
链表的增删改查
推荐使用 哨兵节点 (dummy node),避免处理头节点被删除的特殊情况。
// 哨兵节点写法
ListNode dummy(0, head);
ListNode* cur = &dummy;
while(cur->next != nullptr){
if(cur->next->val == val){
ListNode* tmp = cur->next;
cur->next = cur->next->next;
delete tmp;
} else{
cur = cur->next;
}
}
return dummy.next;利用双指针抵达链表倒数N个元素
快指针先走 n+1 步,这样当快指针抵达 nullptr 时,慢指针恰好在倒数第 n 个元素之前。
反转链表 (K个一组)
// 省略部分代码,展示核心逻辑
while(listSize >= swapSize){
for(int i = 0; i < swapSize; i++){ // 两两交换
ListNode* tmp = cur->next;
cur->next = prv;
prv = cur;
cur = tmp;
}
// 连接前后部分...
}KMP算法
利用模式串自身的前缀/后缀信息(前缀表/LPS),跳过无用比较。
pattern: A B C D A B D
lps: 0 0 0 0 1 2 0
二叉树
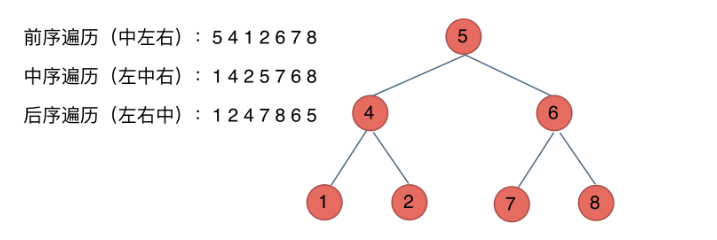
遍历方法
DFS (深度优先)
- 前序: 中左右
- 中序: 左中右
- 后序: 左右中
BFS (广度优先)
层序遍历,使用队列 (Queue)。
迭代遍历 (Stack)
// 前序遍历 (中左右 -> 栈入: 右左)
stack<TreeNode*> st;
st.push(root);
while(!st.empty()){
TreeNode* cur = st.top(); st.pop();
ans.push_back(cur->val);
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}递归寻找公共祖先 (LCA)
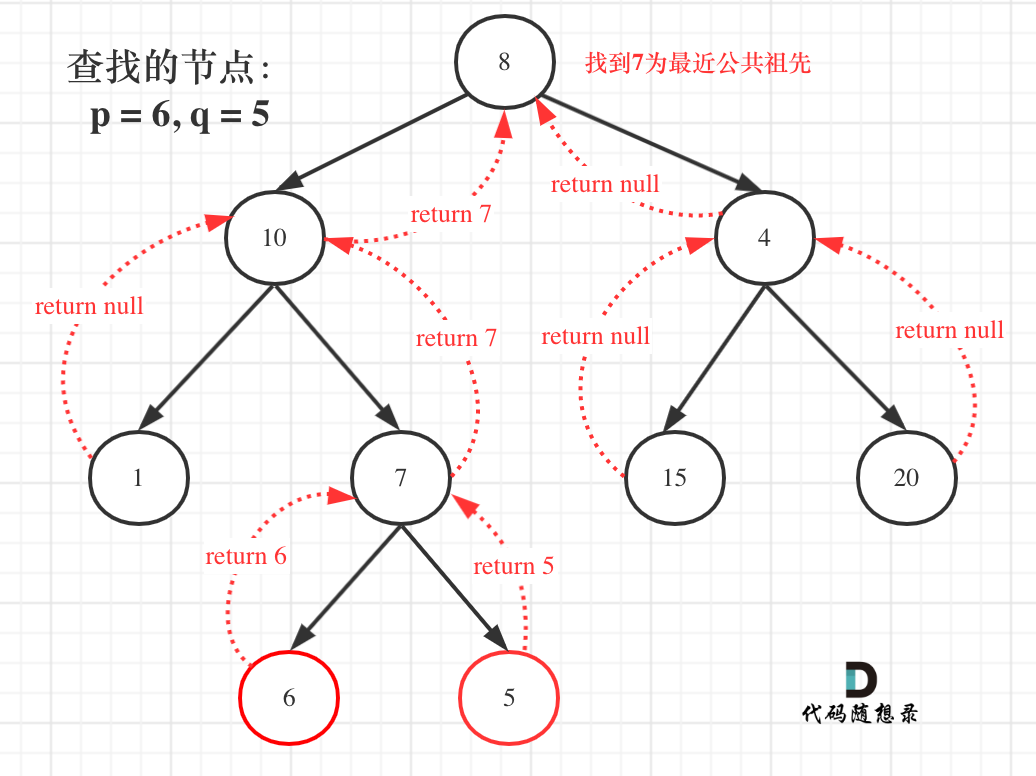
采用后序遍历(自底向上)。如果左右子树返回值都不为空,则当前节点为 LCA。
回溯法
所有回溯法的问题都可以抽象为树形结构。
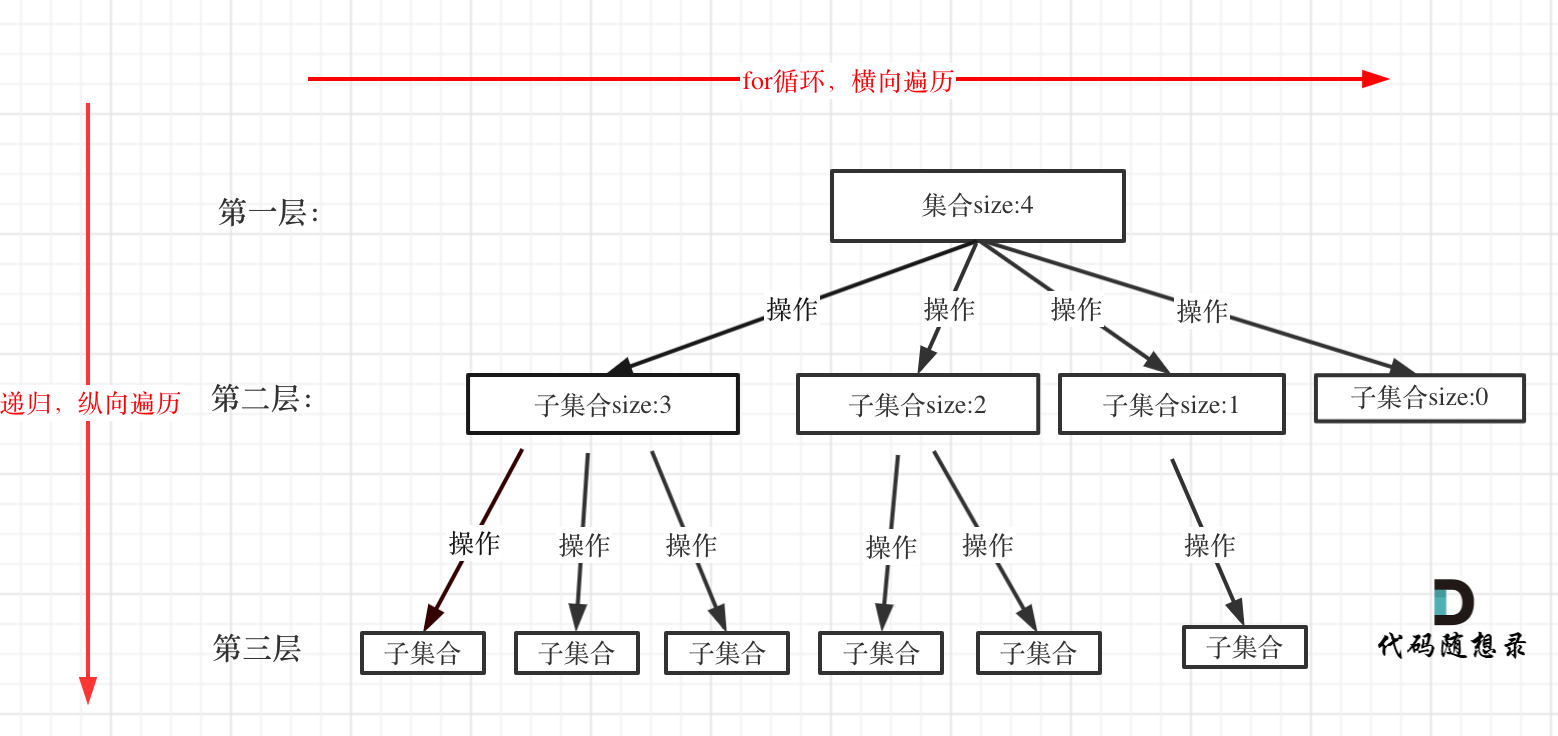
回溯模板
void backtracking(参数) {
if (终止条件) {
存放结果; return;
}
for (选择:本层集合中元素) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果;
}
}去重 (剪枝)

- 树枝去重:同一路径上避免重复使用(排列问题)。使用
used数组。 - 树层去重:同一层避免选相同元素(组合/子集问题)。需要排序,判断
nums[i] == nums[i-1]。
贪心算法
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
解法通常包含:排序解法、后悔解法(优先队列维护)。
动态规划
背包问题

01 背包
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
注意:使用一维数组时,内层循环需从大到小遍历,防止重复放入。
完全背包
- 组合问题 (顺序无关): 外层物品,内层背包。
dp[j] += dp[j - weight[i]] - 排列问题 (顺序有关): 外层背包,内层物品。
单调栈
核心场景:为数组中每个元素寻找左边或右边第一个比它大/小的元素。
while (!st.empty() && nums[i] > nums[st.top()]) {
int top = st.top(); st.pop();
// 逻辑处理:右边界 = i,左边界 = st.top()
}
st.push(i);图论基础
并查集
主要用于解决连通性问题。
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
void join(int u, int v) {
u = find(u); v = find(v);
if (u == v) return;
father[v] = u;
}最小生成树 (MST)
Prim 算法
选点法。适合稠密图。
- 选距离树最近的未访问节点。
- 标记已访问。
- 更新邻居到树的距离 (minDist)。
Kruskal 算法
选边法。适合稀疏图。
- 所有边按权值排序。
- 遍历边,若两点未连通 (并查集 check),则加入。
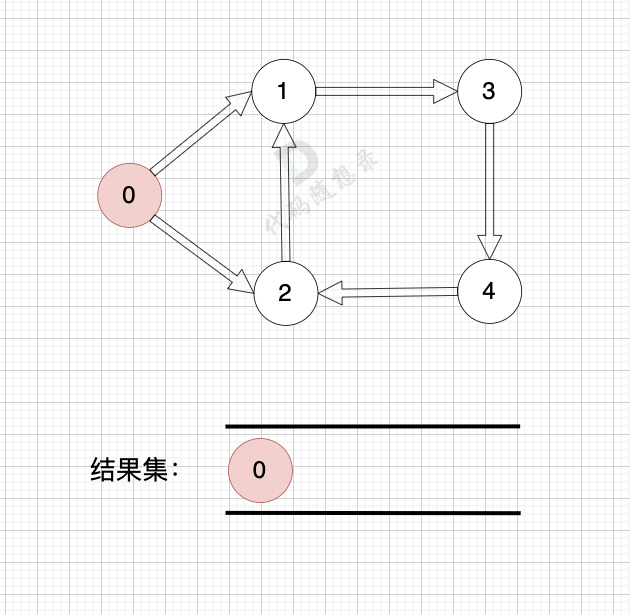
拓扑排序
应用:课程表、依赖解析。
Kahn 算法:维护入度 (In-degree)。将入度为 0 的节点入队,弹出并减少邻居入度,循环直到队列为空。
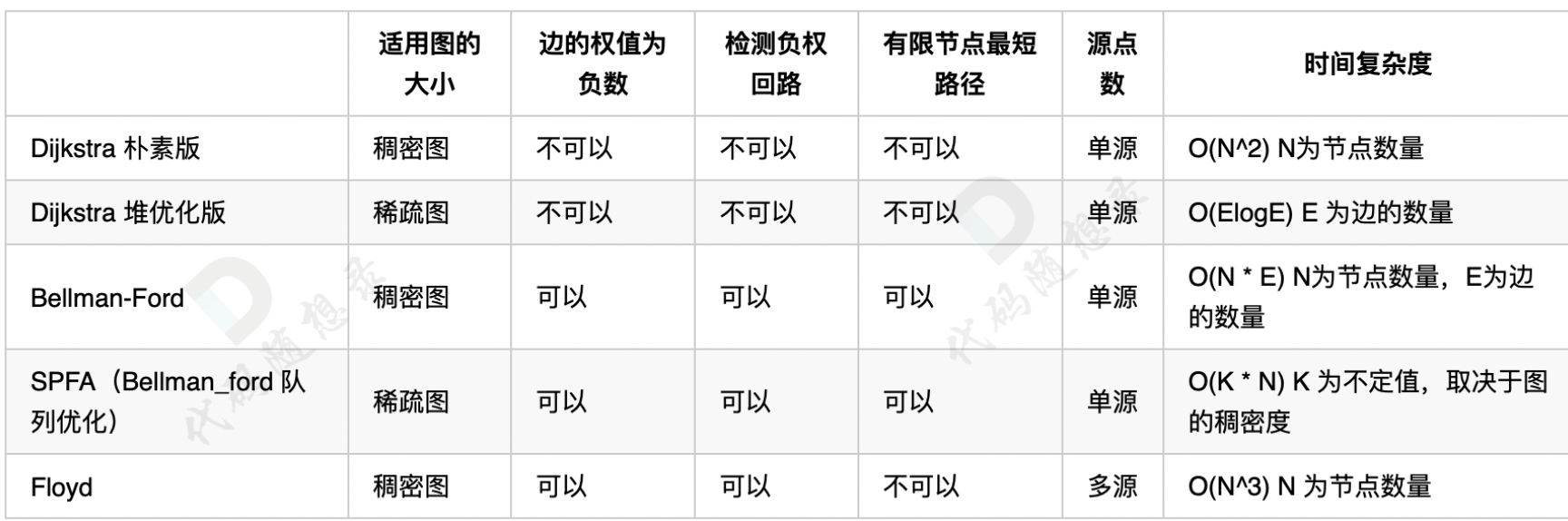
最短路径算法
Dijkstra
贪心 + 优先队列。适用于非负权图。
priority_queue<Node, vector<Node>, greater<Node>> pq; // 小顶堆
pq.push({0, start});
while(!pq.empty()){
// 1. Select
auto [dist, u] = pq.top(); pq.pop();
if(visited[u]) continue;
visited[u] = true; // 2. Finalize
// 3. Relax
for(auto& edge : adj[u]){
if(dist + edge.w < minDist[edge.to]){
minDist[edge.to] = dist + edge.w;
pq.push({minDist[edge.to], edge.to});
}
}
}Bellman-Ford & SPFA
解决负权边。SPFA 是其队列优化版,但最坏情况 O(VE)。
Floyd
多源最短路。动态规划思想。
dp[i][j][k] = min(..., dp[i][k] + dp[k][j])
A* 算法
Dijkstra 的改进版,引入启发式函数 (Heuristic):F = G + H。
- G: 起点到当前的实际代价。
- H: 当前到终点的预估代价(如曼哈顿距离、欧几里得距离)。
struct Node {
int x, y, g, h, f;
bool operator>(const Node& other) const { return f > other.f; } // 小顶堆
};
// 每次优先探索 F 最小的节点